Abstract Link to heading
Intuitively Piecewise Linear Representation refers to the approximation of a time series $T$, of length $n$, with $K$ straight lines. Because $K$ is typically muchsmaller that $n$, this representation makes the storage, transmission and computation of the data more efficient.
The segmentation problem can be framed in several ways.
- Given a time series $T$, produce the best representation using only $K$ segments.
- Given a time series $T$, produce the best representation such that the maximum error for any segment does not exceed some user-specified threshold,
max_error. - Given a time series $T$, produce the best representation such that the combined error of all segments is less than some user-specified threshold,
total_max_error.
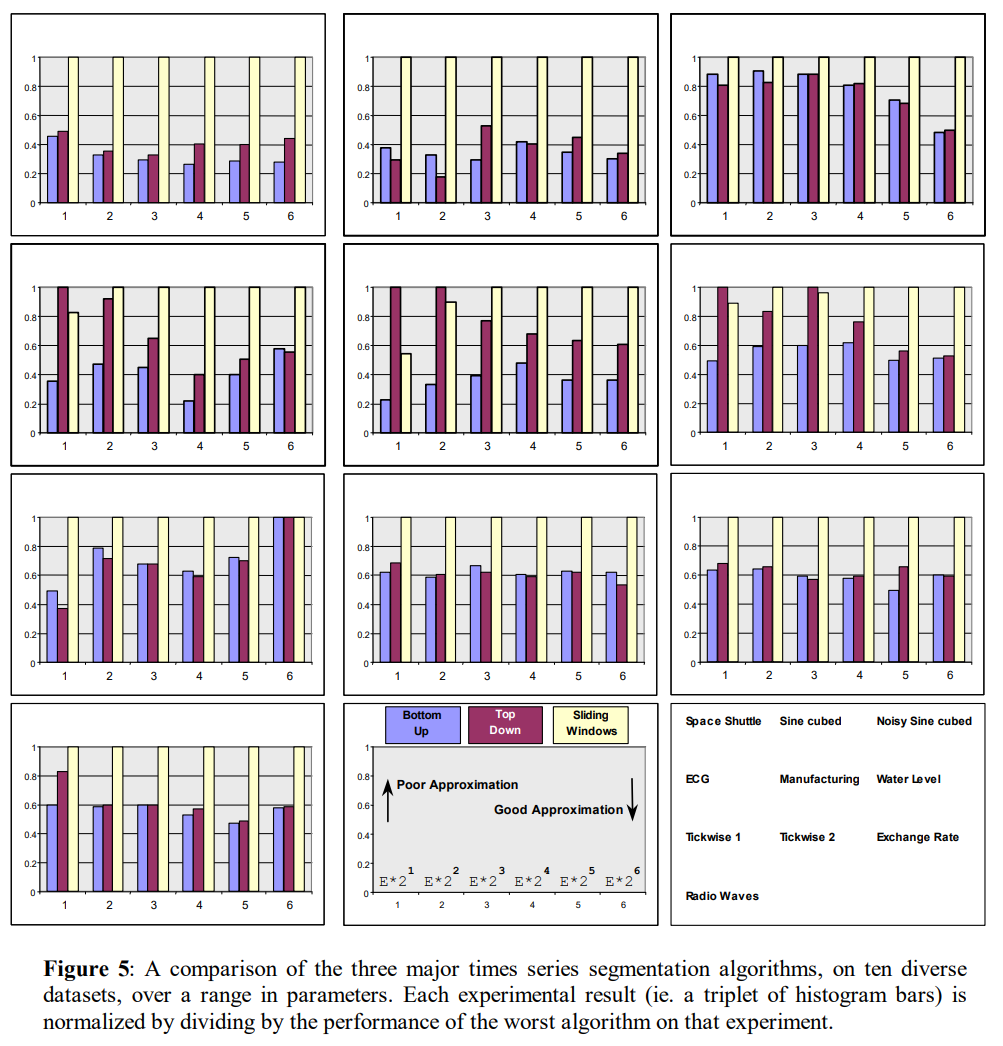
Although appearing under different names and with slightly different implementation details, most time series segmentation algorithms can be grouped into one of the following three categories.
- Sliding Windows: A segment is grown until it exceeds some error bound. The process repeats with the next data point not included in the newly approximated segment.
- Top-Down: The time series is recursively partitioned until some stopping criteria is met.
- Bottom-Up: Starting from the finest possible approximation, segments are merged until some stopping criteria is met.
Given that we are going to approximate a time series with straight lines, there are at least two ways we can find the approximating line.
- Linear Interpolation: Here the approximating line for the subsequence $T[a:b]$ is simply the line connecting $t_{a}$ and $t_{b}$. This can be obtained in constant time.
- Linear Regression: Here the approximating line for the subsequence $T[a:b]$ is taken to be the best fitting line in the least squares sense. This can be obtained in time linear in the length of segment.
The Sliding Window Algorithm Link to heading
The Sliding Window algorithm works by anchoring the left point of a potential segment at the first data point of a time series, then attempting to approximate the data to the right with increasing longer segments. At some point $i$, the error for the potential segment is greater than the user-specified threshold, so the subsequence from the anchor to $i-1$ is transformed into a segment. The anchor is moved to location i, and the process repeats until the entire time series has been transformed into a piecewise linear approximation
Algorithm Seg_TS = Sliding_Window(T , max_error)
anchor = 1;
while not finished segmenting time series
i = 2;
while calculate_error(T[anchor: anchor + i ]) < max_error
i = i + 1;
end;
Seg_TS = concat(Seg_TS, create_segment(T[anchor: anchor + (i-1)]);
anchor = anchor + i;
end;
The Top-Down Algorithm Link to heading
The Top-Down algorithm works by considering every possible partitioning of the times series and splitting it at the best location. Both subsections are then tested to see if their approximation error is below some user-specified threshold. If not, the algorithm recursively continues to split the subsequences until all the segments have approximation errors below the threshold.
Algorithm Seg_TS = Top_Down(T , max_error)
best_so_far = inf;
for i = 2 to length(T) - 2 // Find best place to split the time series.
improvement_in_approximation = improvement_splitting_here(T,i);
if improvement_in_approximation < best_so_far
breakpoint = i;
best_so_far = improvement_in_approximation;
end;
end;
// Recursively split the left segment if necessary.
if calculate_error(T[1:breakpoint]) > max_error
Seg_TS = Top_Down(T[1: breakpoint]);
end;
// Recursively split the right segment if necessary.
if calculate_error(T[breakpoint + 1:length(T)] ) > max_error
Seg_TS = Top_Down(T[breakpoint + 1: length(T)]);
end;
The Bottom-Up Algorithm Link to heading
The Bottom-Up algorithm is the natural complement to the Top-Down algorithm. The algorithm begins by creating the finest possible approximation of the time series, so that $n/2$ segments are used to approximate the n-length time series. Next, the cost of merging each pair of adjacent segments is calculated, and the algorithm begins to iteratively merge the lowest cost pair until a stopping criteria is met. When the pair of adjacent segments $i$ and $i+1$ are merged, the algorithm needs to perform some bookkeeping. First, the cost of merging the new segment with its right neighbor must be calculated. In addition, the cost of merging the $i–1$ segments with its new larger neighbor must be recalculated.
Algorithm Seg_TS = Bottom_Up(T , max_error)
for i = 1 : 2 : length(T) // Create initial fine approximation.
Seg_TS = concat(Seg_TS, create_segment(T[i: i + 1 ]));
end;
for i = 1 : length(Seg_TS) – 1 // Find cost of merging each pair of segments.
merge_cost(i) = calculate_error([merge(Seg_TS(i), Seg_TS(i+1))]);
end;
while min(merge_cost) < max_error // While not finished.
index = min(merge_cost); // Find “cheapest” pair to merge.
Seg_TS(index) = merge(Seg_TS(index), Seg_TS(index+1))); // Merge them.
delete(Seg_TS(index+1)); // Update records.
merge_cost(index) = calculate_error(merge(Seg_TS(index), Seg_TS(index+1)));
merge_cost(index-1) = calculate_error(merge(Seg_TS(index-1), Seg_TS(index)));
end;
Complexity Link to heading

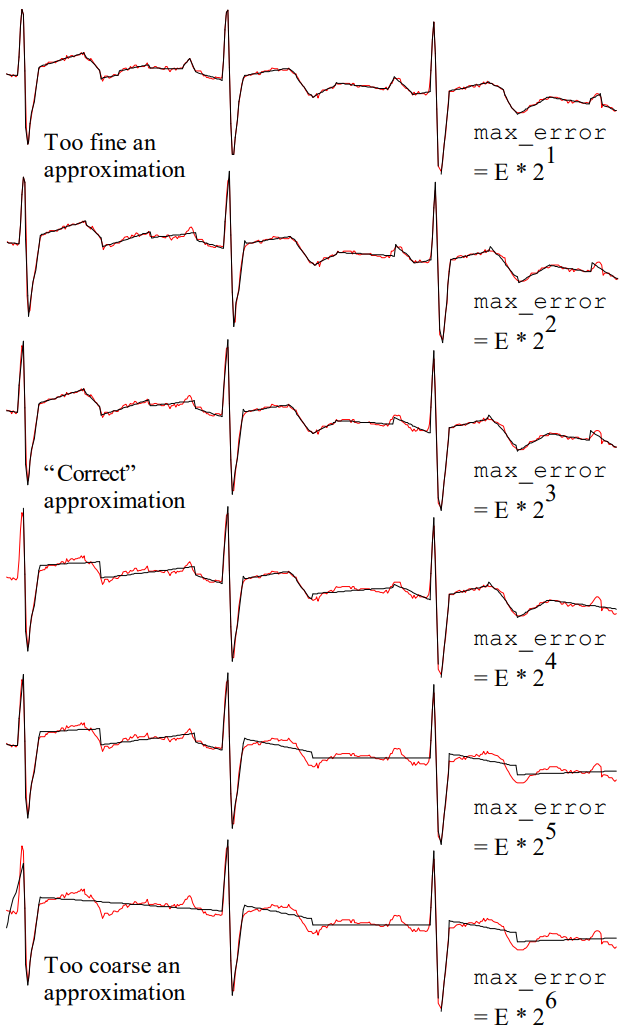
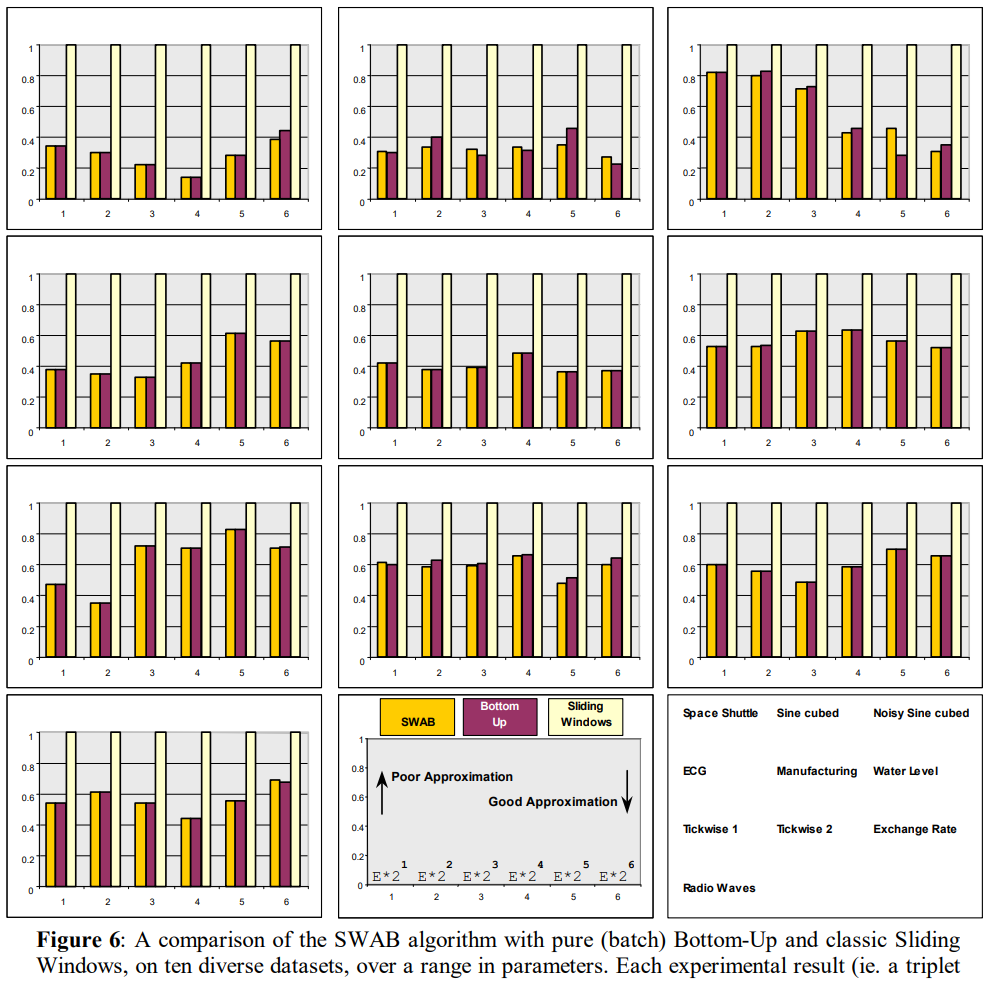
The SWAB Segmentation Algorithm Link to heading
The SWAB algorithm keeps a buffer of size $w$. The buffer size should initially be chosen so that there is enough data to create about 5 or 6 segments. Bottom-Up is applied to the data in the buffer and the leftmost segment is reported. The data corresponding to the reported segment is removed from the buffer and more datapoints are read in. The number of datapoints read in depends on the structure of the incoming data. This process is performed by the Best_Line function, which is basically just classic Sliding Windows. These points are incorporated into the buffer and Bottom-Up is applied again. This process of applying Bottom-Up to the buffer, reporting the leftmost segment, and reading in the next “best fit” subsequence is repeated as long as data arrives (potentially forever).
The intuition behind the algorithm is this. The Best_Line function finds data corresponding to a single segment using the (relatively poor) Sliding Windows and gives it to the buffer. As the data moves through the buffer the (relatively good) Bottom-Up algorithm is given a chance to refine the segmentation, because it has a “semi-global” view of the data. By the time the data is ejected from the buffer, the segmentation breakpoints are usually the same as the ones the batch version of Bottom-Up would have chosen.
Algorithm Seg_TS = SWAB(max_error, seg_num) // seg_num is integer 5 or 6
read in w number of data points // Enough to approximate seg_num of segments.
lower_bound = w / 2;
upper_bound = 2 * w;
while data at input
T = Bottom_Up(w, max_error) // Call the classic Bottom-Up algorithm
Seg_TS = CONCAT(SEG_TS, T(1));
// Sliding window to the right.
w = TAKEOUT(w, w’); // Deletes w’ points in T(1) from w.
if data at input // Add w” points from BEST_LINE() to w.
w = CONCAT(w, BEST_LINE(max_error));
{check upper and lower bound, adjustment if necessary}
else // flush approximated segments from buffer.
Seg_TS = CONCAT(SEG_TS, (T – T(1)))
end;
end;
Function S = BEST_LINE(max_error) //returns S points to approximate
while error <= max_error // next potential segment.
read in one additional data point, d, into S
S = CONCAT(S, d);
error = approx_segment(S);
end while
return S;